ጥግ

በካልኩለስ ጥናት የአንድ አስረካቢ ወይንም ድርድር ግቤት የተወሰነ ዋጋ እየቀረበ ሲሄድ የዚያ አስረካቢ ወይንም ድርድር ውጤት እየተጠጋ የሚሄደው ዋጋ ጥግ ይባላል። ጥግ መሰረታዊ ጽንሰ ሐሳብ እንደመሆኑ ሪጋነት፣ ውድድር እና አጠራቃሚ የተሰኙት የካልኩለስ ዋና ዋና ሃሳቦች የሚተረጎሙት በጥግ ነው፡፡

የአስረካቢ ጥግ

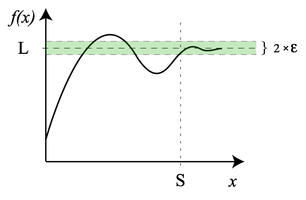
ግቤት x ከ ነጥብ c በ δ ርቅት ላይ ካለ, የf(x) ዋጋ ከጥጉ L በ ε ርቀት ውስጥ ይገኛል። .		ለማናቸውም x > S, አስረካቢ f(x) ከጥግ L በ ε ርቀት ውስጥ ይገኛል

አስረካቢ f(x) እና ነጥብ c ቢሰጡ፣ አስረካቢው በተሰጠው ነጥብ ላይ ሊኖረው የሚችለው ጥግ እንዲህ ይጻፋል

$\lim_{x \to c}f(x) = L$

ትርጉሙም xን ወደ ነጥብ c በማስጠጋት የ አስረካቢ f(x) ዋጋን በተፈለገ መጠን ወደ L ማስጠጋት ይቻላል። እንግዲህ " የx ዋጋው ወደ c ሲጠጋ, የf ጥግ L" ነው ይባላል። በጥንቃቄ መታየተ ያለበት፣ በአንድ ነጥብ ላይ አንድ አስረካቢ ያለው ጥግ እና ውጤት አንድ ላይሆኑ ይችላሉ፣ ማለት f(c) ≠ L። እንዲያውም አስረካቢ f(x) በነጥብ c ላይ ትርጉም ላይኖረውም ይችላል። ጥግ፣ አስረካቢው የሚቀርበውን ዋጋ እንጂ የአስረካቢውን ዋጋ አያሰላም።

ምሳሌ

$f(x) = \frac{x^2 - 1}{x - 1}$

እዚህ ላይ f(1) በዜሮ ማካልፈል ስለሚሆን አስረካቢው 1ን ማስረከብ አይችልም። በሌላ አነጋገር አስረካቢው 1 ላይ ትርጉም የለውም። ሆኖም ግን x ወደ 1 እየተጠጋ ሲሄድ, f(x) ወደ 2 እየተጠጋ ይሄዳል።

f(0.9)	f(0.99)	f(0.999)	f(1.0)	f(1.001)	f(1.01)	f(1.1)
1.900	1.990	1.999	⇒ ትርጉም የለሽ ⇐	2.001	2.010	2.100

ከሰንጠረዡ መረዳት እንደሚቻለው xን ወደ 1 በማስጠጋት አስረካቢ f(x)ን ወደ 2 በፈለግነው መጠን ማስጠጋት ይቻላል። ስለሆነም አስረካቢው በ1 ላይ ያለው ጥግ 2 ነው ይባላል።

ሂሳባዊ የቀኖና ትርጉም

አስረካቢው f(x) በc ላይ ጥግ አለው ሲባል በሂሳብ ቋንቋ እንዲህ ይጻፋል፡ $\lim_{x \to c} f \left( x \right) = L \Leftrightarrow \forall \varepsilon > 0 ~ \exists \delta = \delta \left( \varepsilon \right) ~ \forall x \colon 0 < \left| x - c \right| < \delta \Rightarrow \left| f \left( x \right) - L \right| < \varepsilon$
	የጥግ ቀኖናዊ ትርጉም

የጥግ ባህሪዎች

• እኩልዮሽ

  $\left( \lim_{x \to c} f \left( x \right) = L_1 \right) \land \left( \lim_{x \to c} f \left( x \right) = L_2 \right) \Rightarrow (L_1 = L_2)$

• ቆንጣጭ እርግጥ

• መደመር

  $\left( \lim\limits_{x \to a} f(x) = L \right) \wedge \left( \lim\limits_{x \to a} g(x) = B \right) \Rightarrow \left( \lim\limits_{x \to a} \bigl[f(x)+g(x)\bigr] = L+B \right);$

• መቀነስ

  $\left( \lim\limits_{x \to a} f(x) = L \right) \wedge \left( \lim\limits_{x \to a} g(x) = B \right) \Rightarrow \left( \lim\limits_{x \to a} \bigl[f(x)-g(x)\bigr] = L-B \right);$

• ማባዛት

  $\left( \lim\limits_{x \to a} f(x) = L \right) \wedge \left( \lim\limits_{x \to a} g(x) = B \right) \Rightarrow \left( \lim\limits_{x \to a} \bigl[f(x)\cdot g(x)\bigr] = L\cdot B \right);$

• ማካፈል

  $\left( \lim\limits_{x \to a} f(x) = L \right) \wedge \left( \lim\limits_{x \to a} g(x) = B \neq 0 \right) \Rightarrow \left( \lim\limits_{x \to a} \left[\frac{f(x)}{g(x)}\right] = \frac{L}{B}\right).$