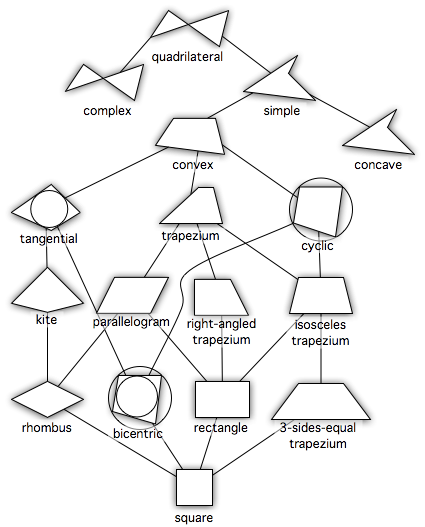
አራት ማዕዘን

አራት ማዕዘን ማናቸውም አራት ቀጥተኛ መስመር የሆኑ "ጎኖች"ና አራት መገናኛወች ያላቸውን የሚወክል የሂሳብ ስያሜ ነው። እኒህ ጎኖች መነባበር ወይም አንዱ ባንዱ ላይ መንሳፈፈ የለባቸውም አለዚያ አራት ማዕዘን አይባሉም።
- የአራት ማዕዘን አራቱ ውስጣዊ ማዕዘኖች ሲደመሩ ምንጊዜም ውጤታቸው 360 ዲግሪ ነው።

ፓራላሎግራም ሁለቱ ጎኑ ትይዩ የሆነ አራት ማዕዘን ፓርላሎግራም ይባላል። በፓራላሎግራም ስር የሚተድዳደሩ እንግዲህ ካሬ፣ ሬክታንግል፣ ሮምበስና ሮምባቶይድ ይባላሉ።
- ሮምበስ ማለት አራቱም ጎኑ እኩል የሆነ ፓራልላሎግራም ነው። በሌላ አነገጋገር ተጻራሪ ጎኖቹ ትይዩ ሲሆኑ ተጻራሪ ማዕዘኖቹ ደግሞ እኩል ናቸው፣ ወይም ደግሞ ዲያጎናሎቹ በ90 ደጊሪ እኩል ለኩል ይቋረጣሉ። ወይም በሌላ አባባል ወደጎን የተገፋ ካሬ ማለት ነው።
- ሮምባቶይድ ማለት ፓራሎግራም ሆኖ ተነካኪ ጎኖቹ እኩል ያልሆኑና ማዕዘኖቹ ኦብሊክ የሆኑ ማለት ነው። በሌላ አባባል የተገፋ ሬክታንግል ማለት ነው።
- ሬክታንግል ማለት አራቱም ማዕዘኖቹ 90ዲግሪ የሆነ አራት ማዕዘን ማለት ነው። በሌላ አባባል ዲያጎናሎቹ እኩል ሆነው እኩል የሚቋረጡ ማለት ነው።
- ካሬ አራቱም ጎኖቹ እኩል የሆኑ እንዲሁም አራቱም ማዕዘኖቹ 90 ዲግሪ የሆኑ ማለት ነው። በአንድ ጊዜ ሮምበስ እና ሬክታንግል የሆነ አራት ማዕዘን ምንጊዜም ካሬ ነው።
እኮሌታ ትራፔዞይድ ሁለቱ ጥንድ ተቃራኒ ጎኖች ትይዩ ከሆኑ የሚፈጠረው አራት ማዕዘን ትራፔዞይድ ይሆናል። ፓራላሎግራም ትራፒዚየም ቢሆንም ትራፒዝየም ግን ፓራላሎግራም አይደለም።
በዚህ መልኩ ብዙ የአራት ማዕዘኖች አይነት እንዳለ እንገነዘባለን።
የተለያዩ ቀመሮች አሉ
አራት ማዕዘን ABCD መጠነ ስፋቱ በቬክተር ሲሰላ እንዲህ ነው፡ ቬክተር AC እና BD ከ A ወደ C እና ከB ወደ D የሚጓዙ ቬክተሮችን ይወክሉ፣ በዚህ ጊዜ የአራት ማዕዘኑ መጠነ ስፋት እንዲህ ነው
ይሄ ማለት ክሮስ ብዜት የምንለው የ AC ና BD መጠነ ቬክተር ውጤት ነው። . በሌላ አጻጻፍ
- ሲሆን p ና q የዲያጎናል ቬክተሮቹ መጠነ ርዝመት ሲሆን . ደግሞ በሁለቱ መካከል ያለው ማዕዘን መጠን ነው [1]
የበርሽናይደር ቀመር የሚባለው ስሌት ደግሞ የማናቸውንም ጎናቸው ወደስጥ የማይገባ አራት ማዕዘኖች መጠነ ስፋት እንዲህ ያስቀምጣል[2] expresses the area in terms of the sides and angles:
- ,
የአራት ማዕዘኑን ጎኖች ርዝመት ሲወክል, ደግሞ የአራት ማዕዘኑ መጠነ ርዝመት ግማሽ ነው። and ማናቸውንም ተቃራኒ ሁለት የአራት ማዐኑ ማዕዘኖችን ይወክላሉ።
በሌላ ወገን ,[3] ጎኖቹንና ዲያጎናሎቹን ብቻ በመውሰድ መጠነ ስፋቱን በዚህ መልኩ ማግኘት እንችላለን
- ,
p ና q እንግዲህ ዲያጎናሎች ናቸው።
ሌሎች መንገዶችም አሉ ሆኖም እነዚህ በቂ ናቸው። እላይ የምናያቸው ቀመሮች የተወሳሰቡ ሊመስሉ ይችላሉ። የተወሳሰቡበት ምክንያት ለማንኛውም መዕዘኑ ወደውስጥ ለማይገባ አራት ማዕዘን ሁሉ ስለሚሰሩ ነው። የፓራላሎግራም፣ በተለይ የሬክታንግልና የካሬ መጠነ ስፋቶች የሚለኩበት ዘዴ እጅግ ሲበዛ ቀላል ነው፡፡
- ^ Harries, J. "Area of a quadrilateral," Mathematical Gazette 86, July 2002, 310-311.
- ^ R. A. Johnson, Advanced Euclidean Geometry, 2007, Dover Publ., p. 82.
- ^ E. W. Weisstein, "Bretschneider's formula," from MathWorld -- A Wolfram Web Resource. http://mathworld.wolfram.com/Bretschneider'sFormula.html




![{\displaystyle Area={\sqrt {(s-a)(s-b)(s-c)(s-d)-{\tfrac {1}{2}}abcd[1+cos(\gamma +\lambda )]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e38ca309f2b07975a5366b30dfe5020995da79e9)
![{\displaystyle ={\sqrt {(s-a)(s-b)(s-c)(s-d)-abcd[cos^{2}({\tfrac {\gamma +\lambda }{2}})]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a7c081b5e8e43c8d4019775d0ee27dacd4dc012)