የጎባጣ ርዝመት

የጎባጣ ርዝመት የምንለው ማናቸውንም ጠማማም ሆነ የተቃና መስመር ርዝመት የምናገኝበትን አጠቃላይ ዘዴን ነው። ይህ ዘዴ በካልኩለስ የሚገኝ ሲሆን አመጣጡም እንዲህ ነው።

ትንሽ የጎባጣ ክፍል, እዚህ ላይ ኢምንት የጎባጣው ክፍል ርዝመት ∆s በ ፓይታጎሪያን መላምት ልትሰላ ትችላለች

የጎባጣውን ርዝመት በቅርብ ለመገመት፣ ጎባጣውን በብዙ ቦታ ከትፎ በቀጥተኛ መስመር መተካት ግድ ይላል።በኋላ የምናገኘውን ውጤት የተቃረበ ግምት ብቻ ሳይሆን ትክክለኛ ዋጋ እንዲሆን ከፈለግን ጎባጣውን በኅልቁ መሳፍርት ቀጥተኛ መስመሮች መተካት ግድ ይላል። እንግዲህ ጎባጣውን የሚተኩት እነዚህ መስመሮች በጣም ጥቃቅን ወይም ኢምንት ናቸው። ስለሆነም እኒህ ኢምንቶችን ደምሮ የተወሰነ ውጤት ለማምጣት የካልኩለስን ሥነ ጥምር መጠቀም አስፈላጊ ነው።

ለምሳሌ አንድ ፈንክሽን $f(x)$ ቢሰጠንና $f(x)$ እና ለውጡ $f'(x)={\frac {dy}{dx}}$ በ [a, b] መካከል ምንም ያልተቆራረጡ ቢሆኑ፣ የዚህ ፈንክሽ በ x = a እና x = b መካከል ያለው ርዝመት s እንዲህ ይሰላል።

እንበልና፣ የጎባጣው ፈንክሽን ኢምንት ክፍል የሆነቸውን $ds$ እንውሰድ። እንደ ፓይታጎረስ መላምት $ds^{2}=dx^{2}+dy^{2}$, ስለሆነም:

$ds^{2}=dx^{2}+dy^{2}$

${\frac {ds^{2}}{dx^{2}}}=1+{\frac {dy^{2}}{dx^{2}}}$

${\frac {ds^{2}}{dx^{2}}}=1+\left({\frac {dy}{dx}}\right)^{2}$

${\frac {ds}{dx}}={\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}$

$ds={\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}dx$

ከዚህ እንግዲህ ዋናውን የጎባጣ ርዝመት መለኪያ ቀመር እናገኛለን።

$s=\int _{a}^{b}{\sqrt {1+[f'(x)]^{2}}}\,dx.$

አንድ ጎባጣ በፓራሜትሪክ ቀመር x = X(t) እና y = Y(t), ከተጻፈ ፣ ከላይ የተጠቀሰውን ቀመር ተጠቅመን ወይም በቀላልይ የፓይታጎረስን መላምት ተጠቅመን ርዝመቱን እንዲህ እናገኛለን

$s=\lim \sum _{a}^{b}{\sqrt {\Delta x^{2}+\Delta y^{2}}}=\int _{a}^{b}{\sqrt {dx^{2}+dy^{2}}}=\int _{a}^{b}{\sqrt {\left({\frac {dx}{dt}}\right)^{2}+\left({\frac {dy}{dt}}\right)^{2}}}\,dt.$

ምሳሌ

ለምሳሌ ከጎን ስዕሉ የተሳለው ፈንክሽን ይሰጠን፡

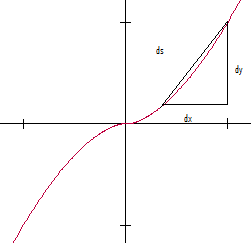ወካይ ቀጥተኛ ክፍል ለፍንክሽን y=t ⁵, x = t ³

${\begin{cases}y=t^{5},\\x=t^{3}.\end{cases}}$

የዚህን ጎባጣ ርዝመት ከ t = -1 እስከ "ቲ" = 1 ማስላት ፈለግን። እንግዲህ ከላይ የተቀመጠውን የፓራሜትሪክ መንገድ በመጠቀም እንዲህ እናገኛለን

$\int _{-1}^{1}{\sqrt {(3t^{2})^{2}+(5t^{4})^{2}}}\,dt=\int _{-1}^{1}{\sqrt {9t^{4}+25t^{8}}}\,dt.$

ይህ ሲሰላ ርዝመቱ 2.905 ሆኖ ይገኛል ማለት ነው፡፡

ማብቂያ የሌለው የትየለሌ ርዝመት

የኮች ጎባጣ

አንድ አንድ ግራፎች የትም ቦታ ቢቆረጡ ቁርጥራጫቸው ምንጊዜም የትየለሌ ርዝመት አለው። ከነዚህ ውስጥ የኮች ጎባጣ አንዱ ሲሆን የ f(x) = x sin(1/x) ግራፍ ሌላው ነው። ሁለተኛው ግራፍ ምንጊዜም የትየለሌ ርዝመት የሚኖረው ዜሮና ሌላ ነጥብ ላይ ከተቆረጠ ነው።