ስፋት ብዜት

ስዕል 1: ወይነ ጠጁ ጨረር የሁለቱ a × b የስፋት ብዜት ውጤት ነው

የስፋት ብዜት በ3 ቅጥ ውስጥ ባሉ ሁለት ጨረሮች (ቬክተሮች) ላይ የሚተገበር የሂሳብ ስሌት ሲሆን ውጤቱም መጠኑ በሁለቱ ጨረሮች መካከል ያለው ፓራሎግራም (አራት ማዕዘን) መጠነ ስፋት የሆነና ለሁለቱ ጨረሮችና አቃፊ ጠለላቸው ቀጤነክ የሆነ ጨረር ነው።

ትርጓሜ

የጂዖሜትሪ ትርጓሜ

የሁለት ቬክተሮችን የስፋት ብዜት ውጤጥ ማግኛ የቀኝ እጅ ደንብ

የስፋት ብዜት

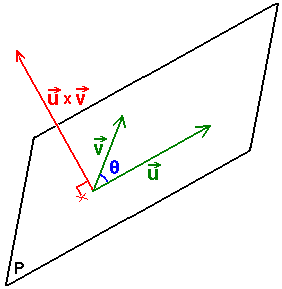
የሁለት ጨረሮች a እና b የስፋት ብዜት እንዲህ ይጻፋል a × b.።

እንግዲህ የስፋት ብዜት በሂሳባዊ ስሌት እንዲህ ይተረጎማል :

$\mathbf {a} \times \mathbf {b} =ab\sin \theta \ \mathbf {n}$

θ እዚህ ላይ በሁለቱ ቬክተሮች መካከል የሚገኝ አንስተኛው ማዕዘን ነው ስለሆነም (0° ≤ θ ≤ 180°)፣ a እና b የቬክተሮቹ a እና b መጠን ናቸው። n ደግሞ መስፈርት ጨረር እንደመሆኑ መጠን ርዝመቱ 1 የሆነ ለሁለቱ ጨረሮችና ለአቃፊ ጠለላቸው ቀጤ ነክ የሆነ ቬክተር ነው። አቅጣጫው ደግሞ በቀኝ እጅ ደንብ የሚገኝ ሲሆን፣ የደንቡ አሰራር ከጎን ባለው ስዕል መሰረት ይካሄዳል። ማለት የቀኝ እጅ ሌባ እጣት ወደ ቬክተር a አቅጣጫ ሲቀሰር፣ የመሃል ጣት ወደ b እንዲያመለክት ይደረጋል። በዚህ ሁኔታ አውራጣት የቬክተር n ን አቅጣጫ ያመለክታል ማለት ነው።

የማትሪክስ ትርጓሜ

የስፋት ብዜት ከላይ ከተጠቀሰው የጂዖሜትሪ ቀመርና ትርጓሜ በተጨማሪ በማትሪክስ እንዲህ ይሰላል፡ ሁለት ጨረሮች ቢሰጡንና አካላቶቻቸው እንዲህ ቢጻፉ

a = a₁i + a₂j + a₃k = (a₁, a₂, a₃)

እና

b = b₁i + b₂j + b₃k = (b₁, b₂, b₃).

የስፋት ብዜታቸው የሚከተለው የማትሪክስ ድርድር-ዋጋ ይሆናል፡

$\mathbf {a} \times \mathbf {b} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\\\end{vmatrix}}.$

ከሊኒያር አልጀብራ ትምህርት እንደሚታወቀው ከላይ የተጠቀሰው ድርድር-ዋጋ እንዲህ ይሰላል

$\mathbf {a} \times \mathbf {b} =\mathbf {i} a_{2}b_{3}+\mathbf {j} a_{3}b_{1}+\mathbf {k} a_{1}b_{2}-\mathbf {i} a_{3}b_{2}-\mathbf {j} a_{1}b_{3}-\mathbf {k} a_{2}b_{1}.$

ስለሆነም

$\mathbf {a} \times \mathbf {b} ={\begin{vmatrix}a_{2}&a_{3}\\b_{2}&b_{3}\end{vmatrix}}\mathbf {i} -{\begin{vmatrix}a_{1}&a_{3}\\b_{1}&b_{3}\end{vmatrix}}\mathbf {j} +{\begin{vmatrix}a_{1}&a_{2}\\b_{1}&b_{2}\end{vmatrix}}\mathbf {k}$

ሙሉ በሙሉ የዚህ ድርድር-ዋጋ ሲተነተን ፡

a × b = (a₂b₃ − a₃b₂) i + (a₃b₁ − a₁b₃) j + (a₁b₂ − a₂b₁) k = (a₂b₃ − a₃b₂, a₃b₁ − a₁b₃, a₁b₂ − a₂b₁).

የስፋት ብዜት ጸባዮች

ጸባይ	ማብራሪያ
የስፋት ብዜት በመደመር ላይ ታዳይ ነው	a × (b + c) = (a × b) + (a × c)
የስፋት ብዜት በስኬላር ሲባዛ እንደማንኛውም ብዜትነው	(r a) × b = a × (r b) = r (a × b)
የጃኮቢ ደንብን ይከተላል	a × (b × c) + b × (c × a) + c × (a × b) = 0
ሁለት መጠናቸው ዜሮ ያልሆኑ ቬክተሮች a እና b ትይዩ የሚሆኑት a × b = 0 ከሆነና ከሆነ ብቻ ነው።	ለምሳሌ <1፣3፣5> እና <4፣5፣7> ትይዩ አይደሉም። ምክንያቱም የስፋት ብዜታቸው <-4፣ 13፣ -7> ስለሆነና 0 ስላልሆነ ነው
i, j, and k መስፈርት ቬክተሮች ሲሆኑ	i × j = k           j × k = i           k × i = j	j × i = −k           k × j = −i           i × k = −j           i × i = j × j = k × k = 0
(a × b) × (a × c) = (a · (b × c)) a	a × (b × c) = b(a · c) − c(a · b)	$(\mathbf {a} \times \mathbf {b} )\cdot (\mathbf {c} \times \mathbf {d} )=(\mathbf {a} \cdot \mathbf {c} )(\mathbf {b} \cdot \mathbf {d} )-(\mathbf {a} \cdot \mathbf {d} )(\mathbf {b} \cdot \mathbf {c} )$
የስፋት ብዜት ኢ-ተገልባጭ ነው	a × b = −b × a	የሁለቱ ተባዦች አደራደር ሲቀያየር ምንም እንኳ የውጤታቸው መጠን ባይቀየርም አቅጣጫው ይገላበጣል
የፓራለልፔፒድ (ጎኖቹ ትይዩ የሆኑ ሳጥን) መጠነ ይዘት በስፋት ብዜትና በነጥብ ብዜት ጥንቅር ይሰላል	$V=|\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|$ ወይም $V=\mathbf {(a\times b)\cdot c} =\mathbf {a\cdot (b\times c)} \$	የሳጥን መጠነ ይዘት በስፋት ብዜትና በነጥብ ብዜት ሲሰላ፣ የተቆራረጡት ነጥቦች የሚያሳዩት የ c ቀጤነክ ጥላ በ a × b ላይ ሲያጠላና የ a ደግሞ b × c ላይ ሲያጠላ ነው